Rabu, 13 Mei 2020
Sabtu, 09 Mei 2020
Luas Permukaan Kubus dan Balok
**LUAS PERMUKAAN
KUBUS DAN BALOK**
A. Luas Permukaan Kubus
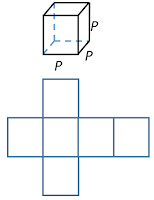
Perhatikan gambar kubus serta salah satu contoh
jaring-jaringnya. Jaring-jaring kubus merupakan
rentangan dari permukaan kubus. Sehingga untuk
menghitung luas permukaan kubus sama dengan
menghitung luas jaring- jaringnya
Karena permukaan kubus terdiri dari enam buah
persegi dengan ukuran yang sama, maka luas kubus
dengan Panjang rusuk p adalah
Luas = 6 x luas persegi
= 6p2
B. Luas Permukaan Balok
Sebuah balok memiliki tiga pasang sisi berupa persegi panjang.
Setiap sisi dan pasangannya saling berhadapan, sejajar, dan kongruen
(sama bentuk dan ukurannya ).
Ketiga pasang sisi tersebut adalah:
1. Sisi atas dan bawah Jumlah luas
= 2 x (p x l)
2. Sisi depan dan belakang Jumlah luas
=2 x (p x t)
3. Sisi kanan dan kiri Jumlah luas
= 2 x (l x t)
Sehingga luas permukaan balok adalah
Total Jumlah ketiga pasang luas sisi-sisi
tersebut.
Contoh soal
Arnol ingin membuat sebuah jaring - jaring balok dari plastik dengan ukuran panjang 20 cm, lebar 18 cm, dan tinggi 10 cm. berapa luas plastik yang dibutuhkan untuk membuat jaring – jaring balok tersebut.
Jawab.
Diketahui
: p = 20 cm
l = 18 cm
t = 10 cm
Ditanya :
Luas = ?
Jawab : L = 2 ( pl + pt + lt )
= 2 ( 20 . 18 + 20 . 10
+ 18 . 10 )
= 2 ( 360 + 200 + 180 )
= 2 ( 740 )
= 1480 cm2
Jadi , plastik transparan yang dibutuhkan seluas 1480 cm2
Sumber: Matematika untuk SMP kelas VIII
Karangan Sukino Wilson Simangunsong
Penerbit Erlangga
Jadi , plastik transparan yang dibutuhkan seluas 1480 cm2
Sumber: Matematika untuk SMP kelas VIII
Karangan Sukino Wilson Simangunsong
Penerbit Erlangga
Balok
** MENGENAL BALOK **
A. Balok
Balok merupakan bangun ruang beraturan yang dibentuk
oleh tiga pasang
persegi panjang yang masing masingnya mempunyai bentuk dan ukuran
yang sama.
persegi panjang yang masing masingnya mempunyai bentuk dan ukuran
yang sama.
Balok mempunyai tiga unsur utama yang merupakan
pembentuk balok
tersebut.
tersebut.
Unsur unsur utama balok itu adalah sisi balok,
rusuk balok, dan titik sudut
balok.
balok.
1.
Sisi Balok
Balok mempunyai tiga pasang sisi, yang masing masing pasang berbentuk persegi panjang yang sama bentuk dan ukurannya.
(
ABCD, EFGH, ABFE, DCGH, ADHE, BCGF adalah sisi balok ABCD.EFGH berdasarkan
gambar di atas)
2.
Rusuk Balok
Balok mempunyai 12 rusuk (AB, DC, EF, HG, AE, BF, CG, DH, AD, BC, EH,dan FG adalah rusuk balok ABCD.EFGH berdasarkan gambar di atas )
3.
Titik Sudut Balok
Titik sudut adalah titik pertemuan dari tiga rusuk kubus yang
berdekatan.
(A, B, C, D, E, F, G, H adalah titik sudut balok ABCD.EFGH
berdasarkan gambar di atas ).
berdasarkan gambar di atas ).
B.Diagonal Balok
1.
Diagonal Sisi ( diagonal bidang )
Balok mempunyai 12 buah diagonal sisi. Diagonal
sisi pada balok
tidak semuanya mempunyai panjang yang sama , bergantung pada
ukuran sisi balok tersebut. Dari gambar terlihat bahwa balok ABCD.
EFGH mempunyai 12 buah diagonal sisi, yaitu AF, BE, CH, DG, AC,
BD, EG, FH, AH, DE, BG, dan CF.
tidak semuanya mempunyai panjang yang sama , bergantung pada
ukuran sisi balok tersebut. Dari gambar terlihat bahwa balok ABCD.
EFGH mempunyai 12 buah diagonal sisi, yaitu AF, BE, CH, DG, AC,
BD, EG, FH, AH, DE, BG, dan CF.
2.
Bidang Diagonal
Bidang
diagonal balok merupakan bidang di dalam balok yang
dibuat melalui dua buah rusuk yang saling sejajar tetapi tidak
terletak pada satu sisi.
dibuat melalui dua buah rusuk yang saling sejajar tetapi tidak
terletak pada satu sisi.
Bidang
diagonal balok berbentuk persegi panjang . Sebuah balok
mempunyai 6 buah bidang diagonal, diantaranya seperti terlihat
pada gambar di atas.
mempunyai 6 buah bidang diagonal, diantaranya seperti terlihat
pada gambar di atas.
3.
Diagonal
Ruang
Balok
ABCD.EFGH mempunyai 4 pasang sudut yang berhadapan,
yaitu A dengan G, B dengan H, C dengan E, dan D dengan F. Jika
titik sudut yang sehadap kita hubungkan maka diperoleh diagonal
ruang balok, yaitu AG, BH, CE, dan DF seperti terlihat pada gambar
di bawah ini.
yaitu A dengan G, B dengan H, C dengan E, dan D dengan F. Jika
titik sudut yang sehadap kita hubungkan maka diperoleh diagonal
ruang balok, yaitu AG, BH, CE, dan DF seperti terlihat pada gambar
di bawah ini.
Sumber: Matematika untuk SMP kelas VIII
Karangan Sukino Wilson Simangunsong
Penerbit ErlanggaKUBUS
MENGENAL KUBUS
A. KUBUS
Kubus merupakan sebuah bangun ruang beraturan yang dibentuk oleh enam buah persegi yang bentuk dan ukurannya sama.
B. UNSUR – UNSUR KUBUS
Kubus mempunyai beberapa unsur utama. Unsur unsur
utama itu adalah sisi, rusuk, dan titik
sudut.
1.
Sisi kubus adalah
suatu bidang persegi (permukaan kubus ) yang membatasi bangun
ruang kubus. Kubus terdiri dari enam sisi yang bentuk dan ukurannya sama.
ruang kubus. Kubus terdiri dari enam sisi yang bentuk dan ukurannya sama.
(ABCD,EFGH,ABFE,DCGH, ADHE,BCGF adalah sisi dari kubus ABCD.EFGH
berdasarkan gambar di atas)
berdasarkan gambar di atas)
2.
Rusuk kubus adalah
ruas garis yang merupakan perpotongan dua bidang sisi pada
sebuah kubus. (AB, BC, CD, DA, EF, FG, GH, HE adalah rusuk kubus ABCD.
EFGH berdasarkan gambar di atas)
sebuah kubus. (AB, BC, CD, DA, EF, FG, GH, HE adalah rusuk kubus ABCD.
EFGH berdasarkan gambar di atas)
3.
Titik sudut adalah
titik pertemuan dari tiga rusuk kubus yang berdekatan.
(A, B, C, D, E, F,
G, H adalah titik sudut kubus ABCD.EFGH berdasarkan
gambar
di atas).
di atas).
C.
DIAGONAL KUBUS
Diagonal merupakan ruas garis yang menghubungkan dua
titik sudut sebidang yang saling berhadapan.
Didalam kubus kita mengenal diagonal sisi ( diagonal bidang), bidang diagonal, dan diagonal ruang.
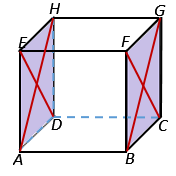
1. Diagonal sisi ( diagonal bidang )
Diagonal sisi kubus adalah diagonal yang terdapat pada sisi kubus.
Pada gambar dibawah terlihat bahwa kubus ABCD.EFGH mempunyai 12 diagonal sisi, yaitu AF, BE, CH, DG, AC, BD, EG, FH, AH, DE, BG, dan CF.
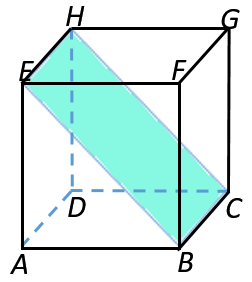
Bidang diagonal merupakan bidang di dalam kubus yang dibuat melalui dua buah rusuk yang saling sejajar tetapi tidak terletak pada satu sisi.
Diagonal ruang adalah ruas garis yang menghubungkan dua titik sudut tidak sebidang yang saling berhadapan.
Ruas garis AG,BH, CE, dan DF disebut diagonal ruang kubus ABCD.EFGH.
1. Diagonal sisi ( diagonal bidang )
Diagonal sisi kubus adalah diagonal yang terdapat pada sisi kubus.
Pada gambar dibawah terlihat bahwa kubus ABCD.EFGH mempunyai 12 diagonal sisi, yaitu AF, BE, CH, DG, AC, BD, EG, FH, AH, DE, BG, dan CF.
2.
BIDANG
DIAGONAL KUBUS
Bidang diagonal merupakan bidang di dalam kubus yang dibuat melalui dua buah rusuk yang saling sejajar tetapi tidak terletak pada satu sisi.
Sebuah kubus mempunyai 6 buah bidang diagonal , diantaranya seperti terlihat pada gambar diatas.
3.
DIAGONAL
RUANG
Diagonal ruang adalah ruas garis yang menghubungkan dua titik sudut tidak sebidang yang saling berhadapan.
Ruas garis AG,BH, CE, dan DF disebut diagonal ruang kubus ABCD.EFGH.
Sumber: Matematika untuk SMP kelas VIII
Karangan Sukino Wilson Simangunsong
Penerbit Erlangga
Langganan:
Komentar (Atom)